Using an LLM to create colour gradients

Did you know you can ask ChatGPT (or whatever) to create RGB Hex values on a colour gradient for you?

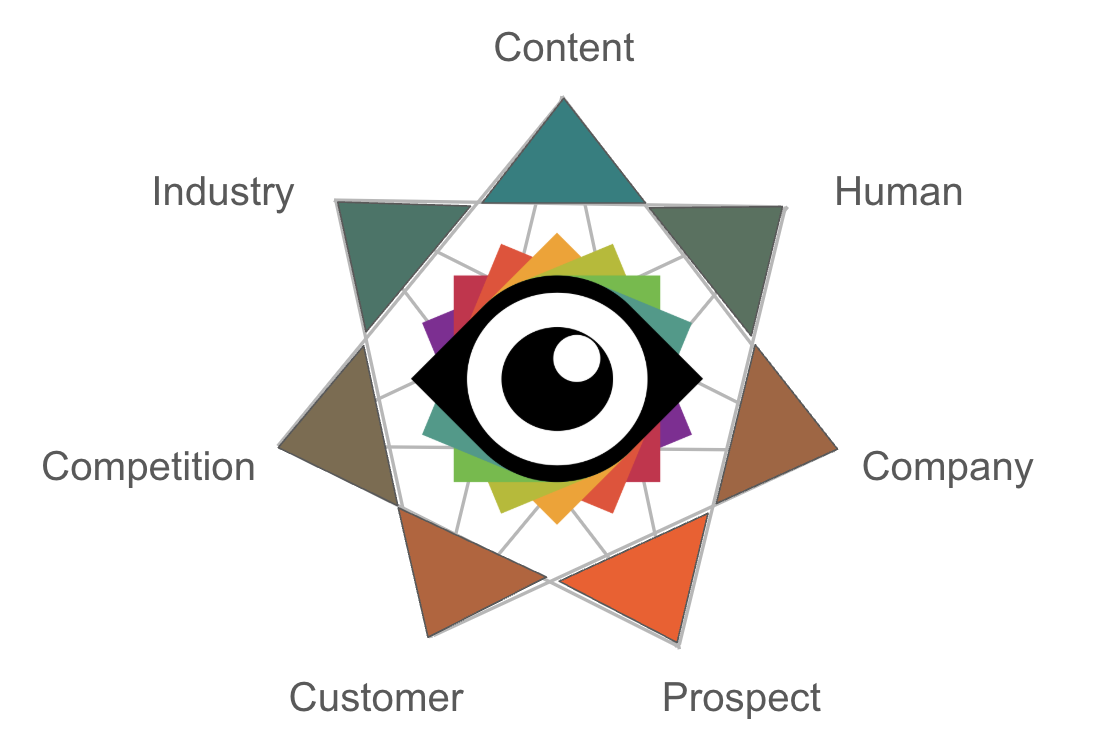
I needed to create this image to explain how content needs to be viewed from seven perspectives. My brand colours are Teal (#008080) and Lobster Red (#FB551C).

First, the image:

Next, how we (ChatGPT and I) did it.

Using ChatGPT o3-mini to create colour gradient values

I’m sure this works fine with other LLMs, but I had o3-mini open so I used that. Here’s the prompt:

I have a seven-segment septagon and want to color each segment with a gradient. The 1st segment colour is teal #008080, and segments 2 and 3 should graduate to segment 4's #fb551c. Then segment's 5 and 6 and 7 should graduate back to the 1st segment's teal.

Now, it didn’t get it correct the first time, but here’s the impressive “reasoning” that ChatGPT o3-mini shared:

Reasoning step

(Reasoned about gradient coloring for septagon for 9 seconds)

Crafting the gradient

I’m working through a seven-segment septagon, using teal (#008080) for segments 1, 5, 6, and 7. Segments 2 and 3 transition through intermediate gradient steps into segment 4’s color, #fb551c.

Pouring details

Segment 1 starts with teal (#008080), transitions through intermediate colors in segments 2 and 3 to #fb551c, and then moves back to teal (#008080) in segments 5, 6, and 7.

Mapping out gradient steps

I’m planning the gradient interpolation between colors teal (#008080) and #fb551c, focusing on segments 2, 3, 5, 6, and 7 for linear interpolation.

Calculating segment colors

I’m figuring out the gradient color segments between teal (#008080) and #fb551c. For segment 2, the interpolated color is #54725F.

Calculating segment colors

I’m thinking through the color for segment 3, finding an approximate hue of #A7633D by interpolating between teal (#008080) and #fb551c.

Calculating segment colors

Piecing together colors for segments 5, 6, and 7, each shares the same interpolated color as segment 3, #A7633D. The gradient moves back from #fb551c to teal (#008080).

Solution synopsis

Below is one way to do it. We start with segment 1 in teal (#008080) and want a smooth gradient from segment 1 to segment 4, ending in #fb551c. Then from segment 4 we “return” back to teal over segments 5–7. (There is a symmetry in the gradient.)

In other words, we want:

• Segment 1: Teal, #008080 (RGB: 0, 128, 128)
• Segments 2 & 3: Gradually changing from teal to the target color
• Segment 4: #fb551c (RGB: 251, 85, 28)
• Segments 5, 6 & 7: Gradually changing from #fb551c back to teal (#008080)

A common method is to linearly interpolate between the two colours. We’ll show one way to do the math.

Solution detail

Gradient from Segment 1 to 4

We have 4 “stops” in total: segments 1, 2, 3, and 4. Think of these as positions at fractions 0, 1/3, 2/3, and 1 of the way from teal to #fb551c.

• Teal (#008080) is (R, G, B) = (0, 128, 128).
• #fb551c is (251, 85, 28).

The change (delta) is:

• ΔR = 251 – 0 = 251
• ΔG = 85 – 128 = –43
• ΔB = 28 – 128 = –100

Now, compute the intermediate colours:

1. Segment 1 (ratio 0):
   RGB=(0, 128, 128)\text{RGB} = (0,\,128,\,128)RGB=(0,128,128) → #008080
2. Segment 2 (ratio 1/3):
   • R: 0+13(251)≈83.670 + \frac{1}{3}(251) \approx 83.670+31​(251)≈83.67 → ~84
   • G: 128+13(−43)≈128−14.33≈113.67128 + \frac{1}{3}(-43) \approx 128 – 14.33 \approx 113.67128+31​(−43)≈128−14.33≈113.67 → ~114
   • B: 128+13(−100)≈128−33.33≈94.67128 + \frac{1}{3}(-100) \approx 128 – 33.33 \approx 94.67128+31​(−100)≈128−33.33≈94.67 → ~95
   In RGB: (84, 114, 95) → In hex, 84 = 54, 114 = 72, 95 = 5F, so #54725F.
3. Segment 3 (ratio 2/3):
   • R: 0+23(251)≈167.330 + \frac{2}{3}(251) \approx 167.330+32​(251)≈167.33 → ~167
   • G: 128+23(−43)≈128−28.67≈99.33128 + \frac{2}{3}(-43) \approx 128 – 28.67 \approx 99.33128+32​(−43)≈128−28.67≈99.33 → ~99
   • B: 128+23(−100)≈128−66.67≈61.33128 + \frac{2}{3}(-100) \approx 128 – 66.67 \approx 61.33128+32​(−100)≈128−66.67≈61.33 → ~61
   In RGB: (167, 99, 61) → In hex, 167 = A7, 99 = 63, 61 = 3D, so #A7633D.
4. Segment 4 (ratio 1):
   Exactly #fb551c (251, 85, 28).

---

Gradient from Segment 4 to 7

Now we have segments 4, 5, 6, and 7. We want to “reverse” the gradient so that:

• Segment 4 is #fb551c (251, 85, 28)
• Segment 7 goes back to teal (#008080) = (0, 128, 128)

The difference (going from segment 4 to segment 7) is:

• ΔR = 0 – 251 = –251
• ΔG = 128 – 85 = 43
• ΔB = 128 – 28 = 100

Again, we use 4 stops (ratios 0, 1/3, 2/3, 1):

1. Segment 4 (ratio 0):
   #fb551c (251, 85, 28)
2. Segment 5 (ratio 1/3):
   • R: 251+13(−251)≈251−83.67≈167.33251 + \frac{1}{3}(-251) \approx 251 – 83.67 \approx 167.33251+31​(−251)≈251−83.67≈167.33 → ~167
   • G: 85+13(43)≈85+14.33≈99.3385 + \frac{1}{3}(43) \approx 85 + 14.33 \approx 99.3385+31​(43)≈85+14.33≈99.33 → ~99
   • B: 28+13(100)≈28+33.33≈61.3328 + \frac{1}{3}(100) \approx 28 + 33.33 \approx 61.3328+31​(100)≈28+33.33≈61.33 → ~61
   That gives (167, 99, 61) which is #A7633D.
3. Segment 6 (ratio 2/3):
   • R: 251+23(−251)≈251−167.33≈83.67251 + \frac{2}{3}(-251) \approx 251 – 167.33 \approx 83.67251+32​(−251)≈251−167.33≈83.67 → ~84
   • G: 85+23(43)≈85+28.67≈113.6785 + \frac{2}{3}(43) \approx 85 + 28.67 \approx 113.6785+32​(43)≈85+28.67≈113.67 → ~114
   • B: 28+23(100)≈28+66.67≈94.6728 + \frac{2}{3}(100) \approx 28 + 66.67 \approx 94.6728+32​(100)≈28+66.67≈94.67 → ~95
   That gives (84, 114, 95) which is #54725F.
4. Segment 7 (ratio 1):
   Finally, back to teal: (0, 128, 128) → #008080.

---

Final Answer

Thus one acceptable set of colours for the seven segments is:

• Segment 1: #008080
• Segment 2: #54725F
• Segment 3: #A7633D
• Segment 4: #FB551C
• Segment 5: #A7633D
• Segment 6: #54725F
• Segment 7: #008080

Any answer that follows this interpolation is correct. Enjoy your gradient septagon!

Correcting o3-mini’s answer

Note that the final answer is (slightly) wrong. Only segment one should be teal… segment 7 should be one-step towards lobster read.

segment 7 shouldn't be teal, it should be the 3rd gradient between segment 4 #FB551C and segment 1 #008080

Reasoning the correction

Reasoned about segment gradient adjustments for 24 seconds

Refining segment specifics

OK, let’s adjust my approach: segment 7 now needs to reflect a gradient between segments 4 (#FB551C) and 1 (#008080), which highlights a continuous transition in segment coloring.

Charting progress

I’m detailing the segments with colors #008080 and #FB551C, noting the adjustment that seg 7 should now reflect the third gradient between the two colors, transitioning smoothly.

Clarifying segment color

OK, let’s clear this up: segment 7 should feature the third gradient between segments 4 (#FB551C) and 1 (#008080), instead of teal.

Clarifying segment coloring

Segment 7 now should show a gradient between segments 4 (#FB551C) and 1 (#008080), not teal, indicating a continuous color transition without ending in teal.

Color progression

Segment 7 will feature the third gradient between #FB551C and #008080, ensuring a seamless transition across the septagon, with teal appearing as the concluding color.

Crafting a continuous gradient

Segment 7 now follows a cyclic gradient from teal at segment 1, through intermediate colors, back to teal, repeating the sequence across segments 1 to 7.

Optimizing color transitions

We’re mapping out the gradient to ensure segment 7 transitions smoothly between segments 4 and 1, with segment 8 featuring teal for a seamless merge across 7 segments.

Mapping gradient flow

Segment 7 follows a transition from segment 4 (#FB551C) to segment 1 (#008080), synthesizing the gradient with segments 5 and 6, and completing the 7-segment cyclic gradient.

Crafting cyclic gradients

I’m aligning the gradient slot positions by assigning segment colors and connections to form a seamless cyclic gradient, ensuring a comprehensive color progression across the septagon.

Mapping the gradient

I’m figuring out the gradient interpolation from teal (#008080) to #FB551C, spanning 7 stops and calculating interpolation ratios for smooth color transitions across segments 1 to 7.

Completing the gradient

I’m finalizing the gradient interpolation for segments 4 to 7, calculating ratios and colors to ensure a smooth transition from #FB551C to teal (#008080) across these segments.

Calculating intermediate colors

I’m mapping out the intermediate color for segment 5 by calculating the RGB values and converting them to their hexadecimal counterparts, ensuring precise color interpolation between #FB551C and teal (#008080).

Advancing the palette

OK, let me see. I’m determining the intermediate colors for segments 5 and 6, converting RGB values to hexadecimal, and ensuring smooth interpolation between #FB551C and teal (#008080) without losing color fidelity.

Finding segment colors

I’m calculating the intermediate colors for segments 6 and 7 by converting RGB values to hexadecimal, ensuring smooth color transitions between #FB551C and teal (#008080). Progress is being made.

Calculating colors

I’m figuring out the RGB values for segments 6 and 7, converting them to hexadecimal, and ensuring a smooth gradient transition between #FB551C and teal (#008080).

Confirming gradient transitions

I’m finalizing the gradient interpolation for segments 2 and 3, ensuring smooth color transitions from teal to #FB551C with RGB values and hexadecimal conversions for each segment.

Updated method synopsis

Below is an updated method that “wraps” the gradient around the septagon so that the cycle starts at segment 1 (teal) and reaches segment 4 (#FB551C), then “returns” back toward teal—but without making segment 7 exactly teal. In other words, if you imagine an 8‑step cyclic gradient (with stop 8 matching segment 1’s teal), then segments 1–7 are as follows:

• Segment 1: Teal (#008080)
• Segments 2 & 3: Transition from teal toward #FB551C
• Segment 4: #FB551C
• Segments 5, 6 & 7: Transition from #FB551C back toward teal (with segment 7 being the third step, not the full teal)

Let’s work through the math.

Revised (correct) solution

Part 1. Gradient from Segment 1 to Segment 4

Imagine there are 4 stops between teal and #FB551C (at segments 1, 2, 3, and 4). Use linear interpolation with these “fractional positions”:

• Segment 1: ratio = 0
• Segment 2: ratio = 1⁄3
• Segment 3: ratio = 2⁄3
• Segment 4: ratio = 1

The two endpoint colours are:

• Teal (#008080): RGB (0, 128, 128)
• #FB551C: RGB (251, 85, 28)

The change (Δ) from teal to #FB551C is:

• ΔR = 251 – 0 = 251
• ΔG = 85 – 128 = –43
• ΔB = 28 – 128 = –100

Now compute the intermediate colours:

1. Segment 1 (ratio 0):
   (0, 128, 128)(0,\,128,\,128)(0,128,128) → #008080
2. Segment 2 (ratio 1⁄3):
   • R: 0+13(251)≈83.670 + \tfrac{1}{3}(251) \approx 83.670+31​(251)≈83.67 → ~84
   • G: 128+13(−43)≈128−14.33≈113.67128 + \tfrac{1}{3}(-43) \approx 128 – 14.33 \approx 113.67128+31​(−43)≈128−14.33≈113.67 → ~114
   • B: 128+13(−100)≈128−33.33≈94.67128 + \tfrac{1}{3}(-100) \approx 128 – 33.33 \approx 94.67128+31​(−100)≈128−33.33≈94.67 → ~95
   RGB: (84, 114, 95) → #54725F
3. Segment 3 (ratio 2⁄3):
   • R: 0+23(251)≈167.330 + \tfrac{2}{3}(251) \approx 167.330+32​(251)≈167.33 → ~167
   • G: 128+23(−43)≈128−28.67≈99.33128 + \tfrac{2}{3}(-43) \approx 128 – 28.67 \approx 99.33128+32​(−43)≈128−28.67≈99.33 → ~99
   • B: 128+23(−100)≈128−66.67≈61.33128 + \tfrac{2}{3}(-100) \approx 128 – 66.67 \approx 61.33128+32​(−100)≈128−66.67≈61.33 → ~61
   RGB: (167, 99, 61) → #A7633D
4. Segment 4 (ratio 1):
   #FB551C (251, 85, 28)

---

Part 2. Gradient from Segment 4 Back Toward Teal

Now, rather than having segment 7 land exactly on teal, we’ll “reserve” the full teal for what would be stop 8 (which matches segment 1 in a cyclic design). In other words, we have 5 stops from segment 4 back to teal:

• Stop 0: Segment 4 (ratio = 0) → #FB551C
• Stop 1: Segment 5 (ratio = 0.25)
• Stop 2: Segment 6 (ratio = 0.5)
• Stop 3: Segment 7 (ratio = 0.75)
• Stop 4: (Not used on the septagon, but would be segment 8) → Teal (#008080)

The change from #FB551C to teal (#008080) is computed by subtracting:

• Start (#FB551C): RGB (251, 85, 28)
• End (teal): RGB (0, 128, 128)
• Δ: (0 – 251, 128 – 85, 128 – 28) = (–251, +43, +100)

Now calculate the intermediate colours:

1. Segment 5 (ratio 0.25):
   • R: 251+(−251×0.25)=251−62.75≈188.25251 + (-251 \times 0.25) = 251 – 62.75 \approx 188.25251+(−251×0.25)=251−62.75≈188.25 → ~188
   • G: 85+(43×0.25)=85+10.75≈95.7585 + (43 \times 0.25) = 85 + 10.75 \approx 95.7585+(43×0.25)=85+10.75≈95.75 → ~96
   • B: 28+(100×0.25)=28+25=5328 + (100 \times 0.25) = 28 + 25 = 5328+(100×0.25)=28+25=53
   RGB: (188, 96, 53)
   • 188 → BC (hex)
   • 96 → 60 (hex)
   • 53 → 35 (hex)
   Hex: #BC6035
2. Segment 6 (ratio 0.5):
   • R: 251+(−251×0.5)=251−125.5≈125.5251 + (-251 \times 0.5) = 251 – 125.5 \approx 125.5251+(−251×0.5)=251−125.5≈125.5 → ~126
   • G: 85+(43×0.5)=85+21.5≈106.585 + (43 \times 0.5) = 85 + 21.5 \approx 106.585+(43×0.5)=85+21.5≈106.5 → ~107
   • B: 28+(100×0.5)=28+50=7828 + (100 \times 0.5) = 28 + 50 = 7828+(100×0.5)=28+50=78
   RGB: (126, 107, 78)
   • 126 → 7E (hex)
   • 107 → 6B (hex)
   • 78 → 4E (hex)
   Hex: #7E6B4E
3. Segment 7 (ratio 0.75):
   • R: 251+(−251×0.75)=251−188.25≈62.75251 + (-251 \times 0.75) = 251 – 188.25 \approx 62.75251+(−251×0.75)=251−188.25≈62.75 → ~63
   • G: 85+(43×0.75)=85+32.25≈117.2585 + (43 \times 0.75) = 85 + 32.25 \approx 117.2585+(43×0.75)=85+32.25≈117.25 → ~117
   • B: 28+(100×0.75)=28+75=10328 + (100 \times 0.75) = 28 + 75 = 10328+(100×0.75)=28+75=103
   RGB: (63, 117, 103)
   • 63 → 3F (hex)
   • 117 → 75 (hex)
   • 103 → 67 (hex)
   Hex: #3F7567

---

Final Colours for Each Segment

Putting it all together, your septagon’s colours are:

• Segment 1: #008080
• Segment 2: #54725F
• Segment 3: #A7633D
• Segment 4: #FB551C
• Segment 5: #BC6035
• Segment 6: #7E6B4E
• Segment 7: #3F7567

With these choices, the gradient smoothly goes from teal at segment 1 up to #FB551C at segment 4, and then gradually returns toward teal over segments 5–7—but note that the teal isn’t repeated at segment 7. (If the cycle were to continue, segment 8—coinciding with segment 1—would be teal again.)

Feel free to adjust the rounding if you’d like slightly different values, but this is one consistent way to meet your updated requirement. Enjoy your gradient septagon!